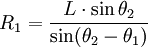曲线拟合的定义
曲线拟合是指用连续曲线近似地刻画或比拟平面上离散点组所表示的坐标之间的函数关系。推求一个解析函数y=f(x)使其通过或近似通过有限序列的资料点(xi,yi),通常用多项式函数通过最小二乘法求得此拟合函数。
曲线拟合的分析
用连续曲线近似地刻画或比拟平面上离散点组所表示的坐标之间的函数关系。更广泛地说,空间或高维空间中的相应问题亦属此范畴。在数值分析中,曲线拟合就是用解析表达式逼近离散数据,即离散数据的公式化。实践中,离散点组或数据往往是各种物理问题和统计问题有关量的多次观测值或实验值,它们是零散的,不仅不便于处理,而且通常不能确切和充分地体现出其固有的规律。这种缺陷正可由适当的解析表达式来弥补。
数学表述 设给定离散数据
(
x
k,
y
k) (k=1,2,…,m),(1)
式中
x
k为自变量x(标量或向量,即一元或多元变量)的取值;
y
k为因变量 y(标量)的相应值。曲线拟合要解决的问题是寻求与(1)的背景规律相适应解析表达式
y=f(x,b),(2)
使它在某种意义下最佳地逼近或拟合(1),?(x,b)称为拟合模型;为待定参数,当b)仅在?中线性地出现时,称模型为线性的,否则为非线性的。量
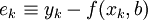
(k=1,2,…,m)
称为在
x
k处拟合的残差或剩余,衡量拟合优度的标准通常有
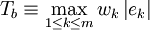
或
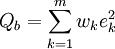
式中ωk>0为权系数或权重(如无特别指定,一般取为平均权重,即
w
k(k=1,2,…,m),此时无需提到权)。当参数b)使T(b))或Q(b))达到最小时,相应的(2)分别称为在加权切比雪夫意义或加权最小二乘意义下对 (1)的拟合,后者在计算上较简便且最为常用。
模型中参数的确定 一般的线性模型是以参数 b)为系数的广义多项式,即
f(x,b)=
b0
g0(x)+
b1
g1(x)+…
b
n
g
n(x) (3)
式中g0,g1,…,gn称为基函数。对诸gj的不同选取可构成多种典型的和常用的线性模型。从函数逼近的观点来看,式(3)还能近似地体现许多非线性模型的性质。
在最小二乘意义下用线性模型(3)拟合离散点组(1),参数b可通过解方程组
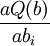
=0(i=0,…,n)来确定,即解关于b0,b1,…,bn的线性代数方程组
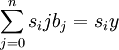
(i=0,1,…,n), (4)
式中
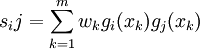
(i,j=0,1,…,n),
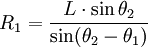
方程组(4)通常称为法方程或正规方程,当m>n时一般有惟一解。
至于非线性模型以及非最小二乘原则的情形,参数b)可通过解非线性方程组或最优化计算中的有关方法来确定(见非线性方程组数值解法、最优化)。
模型的选择
对于给定的离散数据(1),需恰当地选取一般模型(2)中函数f(x,b)的类别和具体形式,这是拟合效果的基础。若已知(1)的实际背景规律,即因变量y对自变量 x的依赖关系已有表达式形式确定的经验公式,则直接取相应的经验公式为拟合模型。反之,可通过对模型(3)中基函数g0,g1,…,gn(个数和种类)的不同选取,分别进行相应的拟合并择其效果佳者。函数g0,g1,…,gn对模型的适应性起着测试的作用,故又称为测试函数。另一种途径是:在模型(3)中纳入个数和种类足够多的测试函数,借助于数理统计方法中的相关性分析和显著性检验,对所包含的测试函数逐个或依次进行筛选以建立较适合的模型(见回归分析)。当然,上述方法还可对拟合的残差(视为新的离散数据)再次进行,以弥补初次拟合的不足。总之,当数据中变量之间的内在联系不明确时,为选择到相适应的模型,一般需要反复地进行拟合试验和分析鉴别。
标签:
投资说 » 曲线拟合
免责声明:本文由网友提供互联网分享,不代表本网的观点和立场;如有侵权请联系删除。
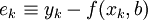 (k=1,2,…,m)
(k=1,2,…,m)
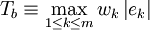 或
或
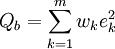
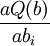 =0(i=0,…,n)来确定,即解关于b0,b1,…,bn的线性代数方程组
=0(i=0,…,n)来确定,即解关于b0,b1,…,bn的线性代数方程组
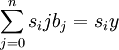 (i=0,1,…,n), (4)
(i=0,1,…,n), (4)
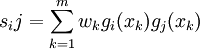 (i,j=0,1,…,n),
(i,j=0,1,…,n),